Cinématique du point matériel
1-Introduction
La plupart des objets étudiés par les physiciens sont en mouvement : depuis les particules élémentaires telles que les électrons, les protons et les neutrons qui constituent les atomes, jusqu’aux galaxies, en passant par les objets usuels et les corps célestes.
La branche de la physique qui étudie les mouvements s’appelle la mécanique.
La cinématique est la partie de la mécanique qui permet d’étudier et de décrire les mouvements des corps, d’un point de vue purement mathématique, indépendamment des causes qui les produisent.
La dynamique, en revanche, s’intéresse à ces causes : les forces. Elle relie les forces au mouvement.
Pour résumer, on peut noter :
Mécanique = Cinématique + Dynamique
L’analyse des grandeurs cinématiques (position, vitesse et accélération) permet de déterminer la géométrie et les dimensions des composants d’un mécanisme.
La cinématique, combinée à l’étude des actions mécaniques, permet l’application du principe fondamental de la dynamique (non étudié ici).
Exemples :
- Usinage : trajectoire d’un outil, vitesse d’avance …
- Dimensionnement d’une pompe : cylindrée, débit …
1-1. Limites de ce cours
A. Le point matériel ou particule.
Un point matériel est un modèle commode pour représenter un corps physique réel. Ce modèle est valable si les dimensions du corps physique sont faibles par rapport à la distance d’observation (de celui qui observe le mouvement).
Par exemple, la navette spatiale peut-être assimilée à un point matériel pour un observateur terrestre mais pas pour son commandant de bord. En effet pour ce dernier, la navette a des dimensions spatiales, elle peut tourner sur elle-même etc…
B. Le solide indéformable.
Nous allons supposer dans ce cours que les solides, corps physiques massiques constitués d’atomes et de molécules, sont indéformables.
Dans ce cas, tous les points du solides garderont des distances respectives inchangées au cours du temps.
Il s’agit d’un modèle idéalisé, qui est très pertinent dans de nombreux cas.
Cependant, les ingénieurs et les scientifiques savent que les matériaux, même solide, se déforment et il faut en tenir compte, notamment dans la construction des infrastructures.
2-Historique
XVIIème Siècle
- Galilée, introduction de la notion de vitesse et du mouvement uniformément accéléré en termes précis. Utilisation du langage mathématiques pour décrire la nature.
- 1687 : Newton publie « Les principes mathématiques de la philosophie naturelle », fondement de la mécanique classique, notions de force, d’accélération, de gravitation etc…
Newton formalisa plus rigoureusement l’idée d’un temps absolu , dans lequel il fonde sa mécanique et où le temps devient une variable mathématique notée t.
Le postulat que fait Newton est de réduire le temps à une variable scalaire (à une dimension donc) qui croît continûment, ceci indépendamment de tout observateur et de tout phénomène.
Cette variable permet alors d’ordonner les événements observés pour produire une chronologie.
La chronologie, dans ce contexte, devient alors absolue puisque le temps s'écoule de la même manière pour tout observateur.
Pour les mêmes raisons, la notion de simultanéité est absolue.
La course du temps est en général représentée par un axe orienté qui indique le futur.
Cet axe est linéaire et non circulaire pour respecter un principe fondamental de physique qui, jusqu’ici, n’a jamais été infirmé : le Principe de Causalité.
Principe de Causalité La cause est, pour tout observateur, antérieure à l’effet qu’elle produit. De manière plus générale, la chronologie de deux événements reliés causalement est toujours la même, quel que soit l’observateur.
Début du XXème siècle
- 1905 : Einstein publie la théorie de la relativité restreinte (sans oublier les travaux précurseurs de Poincaré et Lorentz). C’est la remise en cause de la mécanique de Newton (la vitesse de la lumière est constante, le temps n’est plus absolu, concept d’espace-temps…).
- 1916 : Einstein publie la théorie de la relativité générale. Les objets massifs déforment l’espace-temps, explication géométrique de la gravité.
De 1900 à 1930
- Élaboration de la mécanique quantique (Shrödinger, Heisenberg, Bohr, De Broglie), remise en cause de la notion de vitesse et de position, description des particules en termes de probabilité de présence.
De 1930 à 1950
- Élaboration d’une mécanique quantique et relativiste (Dirac, Pauli, Feynman, Schwinger, Tomonaga).
3-Définitions
3.1 - Repère d’espace
On appelle repère d’espace un ensemble de points dont les distances sont invariables au cours du temps.
Un tel ensemble est aussi appelé un solide de référence. Par exemple une table, un bateau, la terre peuvent servir de repère d’espace.
3.2 - Système de coordonnées
On exprime la position d’un objet par rapport à un système de coordonnées qui est constitué d’un ensemble de trois axes dont chacun correspond à une direction de l’espace et qui est considéré comme fixe par rapport à un repère d’espace.
On dit que le système de coordonnées est lié au repère.
Dans la suite, nous allons utiliser les systèmes de coordonnées suivants :
- Cartésien
- Polaire (cylindrique à 2D)
- Cylindrique
- Sphérique
3.3 - Référentiel
Un ensemble formé d’un repère d’espace et d’un repère de temps (un ensemble d’horloges synchronisées) constitue un référentiel, c’est–à-dire une référence spatiale et une référence temporelle, toutes deux indispensables dans l’étude de tout mouvement.
Référentiel = Repère d’espace + Repère de temps
Observons un Individu (A) immobile sur un escalator.
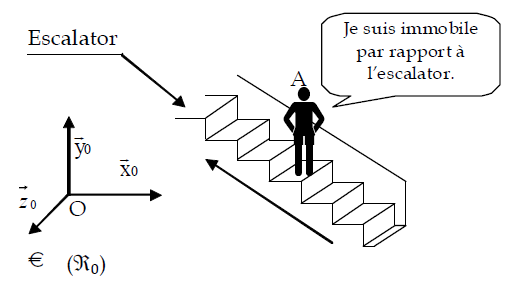
Le repère ℜ0 est lié au sol.
L’individu A est mobile dans le repère ℜ0, mais immobile par rapport à l’escalator.
L’étude de tout mouvement implique deux solides en présence :
- Le solide (S) dont on étudie le mouvement.
- Le solide (S0) par rapport auquel on définit le mouvement.
Le solide (S0) est appelé solide de référence, auquel on associe le repère de référence ℜ0.
Le mouvement du solide (S) par rapport au solide (S0) est noté Mvt S/S0.
Quelle que soit l’étude cinématique à réaliser, on a toujours besoin de la situer dans le temps.
On appelle instant t ou date t le temps écoulé depuis une origine des temps t0=0, choisie arbitrairement.
L’unité de mesure du temps (système ISO) est la seconde, notée s.
La grandeur Δt = t2-t1 est appelée durée entre les deux instants t1 et t2.
3.4 - Trajectoire
On appelle trajectoire du point (M) d’un solide (S) l’ensemble des positions occupées successivement par ce point, au cours du temps, et au cours de son déplacement par rapport à un référentiel donné.
Une trajectoire est donc représentée par une courbe (C).
Cette trajectoire sera notée : TM∈S/R0 : trajectoire du point M appartenant à S, par rapport au repère ℜ0.
Remarque : Il est, parfois, plus judicieux de remplacer le terme « appartenant à » par « accroché à » pour avoir une meilleure visualisation de la trajectoire…