Stock de sécurité

Détermination du stock de sécurité

Si la demande et l'offre sont volatile et variable, le stock de sécurité permet d'améliorer la disponibilité des produits dans la Supply Chain.

graphique simple illustrant le point de commande

graphique complet illustrant le point de commande

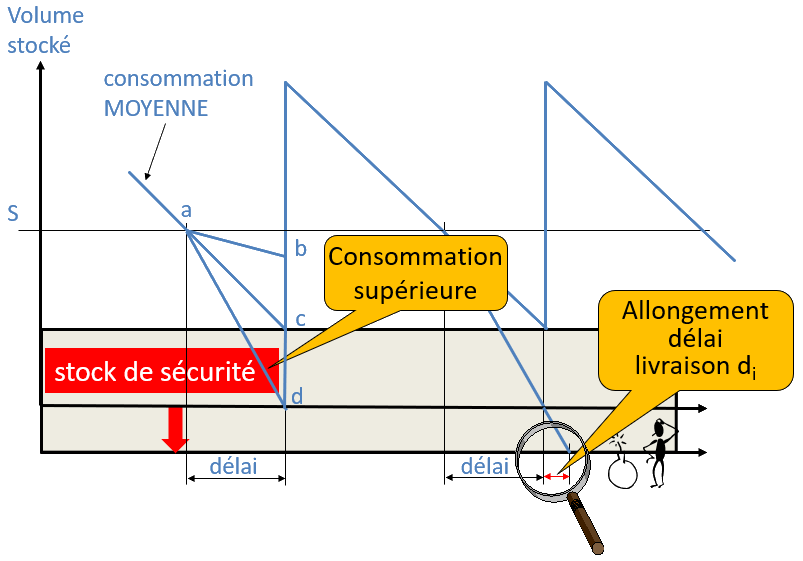
Si on augmente le délai le stock de sécurité augmente également.

graphique complet illustrant le point de commande avec le stock de sécurité

Pourquoi un stock de sécurité ?

Stock de sécurité: Quantité de stock prévue pour protéger contre les fluctuations de demande ou de livraison.

Demande dépendante : se protéger contre les variations du délai fournisseur ou rebuts de production.

Demande indépendante : se protéger contre la variation de la demande

Variabilité

La variabilité peut se traduire sous deux formes :

Quantité : stock de sécurité
Délai : délai de sécurité

On peut également trouver d'autres éléments influençant :

Variabilité de la demande pendant le délai de réapprovisionnement.
Fréquence de réapprovisionnement.
Niveau de service souhaité.
Longueur du délai.

Plus le délai est long, plus le niveau du stock de sécurité est important, c'est pourquoi il faut réduire les délais.

Plus on alimente fréquemment, plus les risques de ruptures sont importants.

Dans tous les cas, il faut connaître les distributions de probabilité.

Si la demande indépendante sur un article suit une loi normale (courbe de Gauss), on peut déterminer le stock de sécurité par calcul.

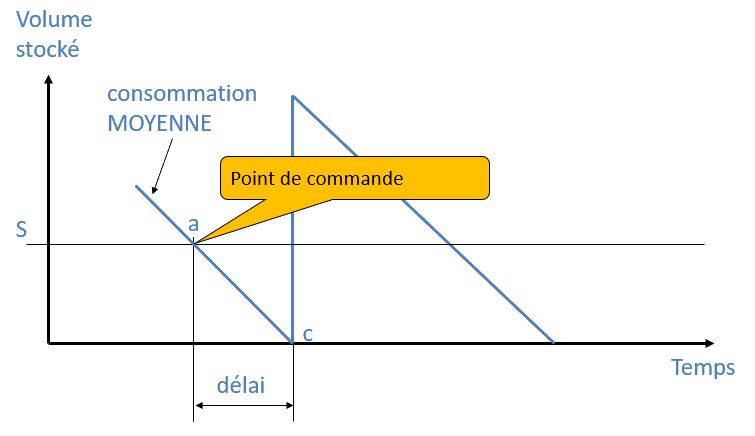
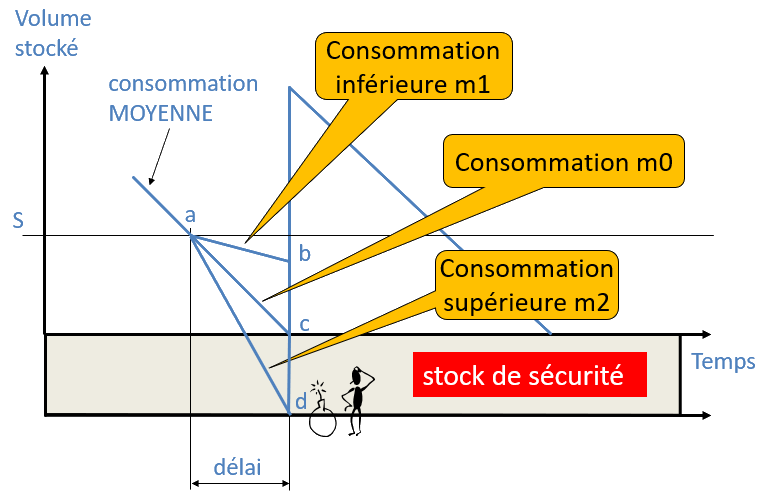
Les seuils de commande sont déterminés à partir des délais et des consommations moyennes (c). Si la consommation est inférieure à la moyenne (b) cela va faire monter, momentanément, le niveau du stock. Si la consommation est supérieure à la moyenne (d) cela provoquera une rupture de stock.

C'est pour se prémunir de cette rupture que l'on mettra en place un stock de sécurité.

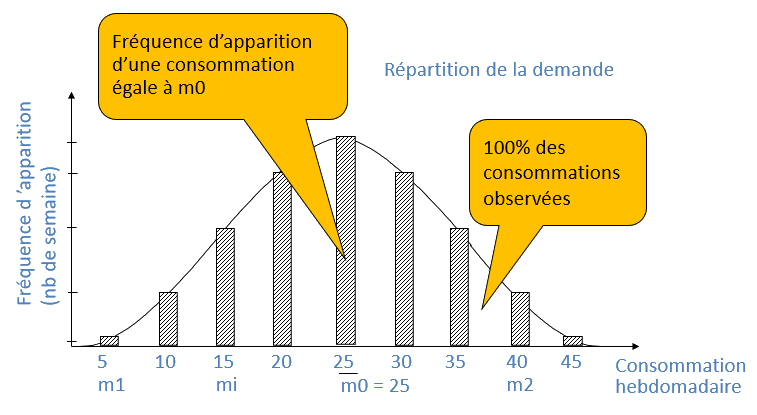
Répartition de la demande

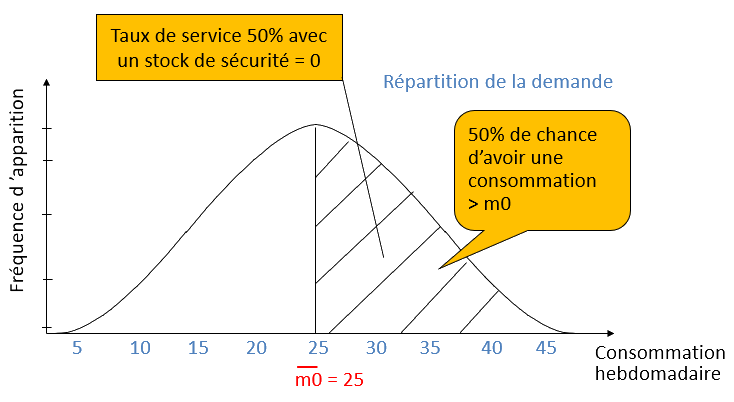
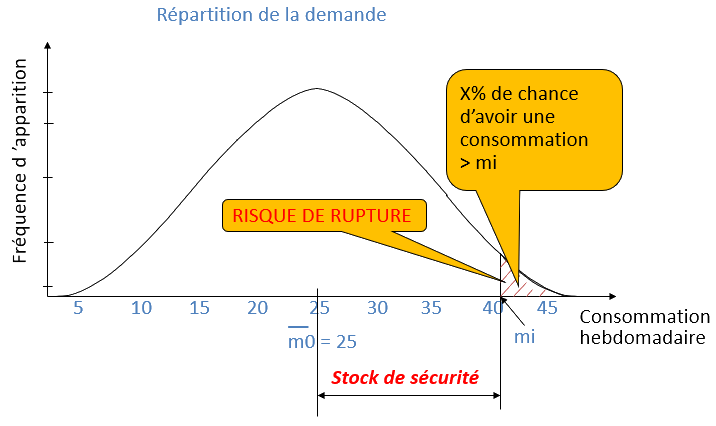
Courbe de Gauss montrant la zone de risque de rupture

L'importance du stock de sécurité dépendra du niveau de service que l'on veut obtenir.

Si le stock de sécurité est égal à 0, nous aurons un taux de service de 50%. Il est possible de calculer le taux de service que l'on peut obtenir, en connaissant le nombre d'écart-type de produits que l'on a en stock de sécurité.

Si la répartition est normale, on pourra calculer l'écart-type (𝜎) selon la formule :

𝜎 = √

ⁿ Σ _i=1

(X_i - X)² / n

L'écart-type est la racine carré de la variance.

Comment interpréter la variance ?

La variance est la dispersion des valeurs par rapport à la moyenne.

Concrètement, la variance est définie comme la moyenne des carrés des écarts à la moyenne.

La considération du carré de ces écarts évite que s'annulent des écarts positifs et négatifs.

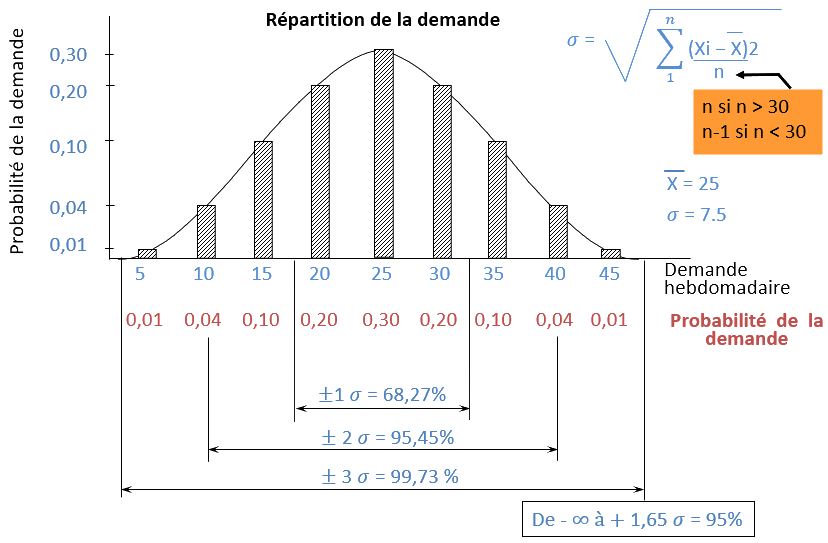
Courbe de Gauss montrant la probabilité de la demande en %

Dans notre exemple, la distribution de la demande est donnée :

Demande de 5 articles/période : 1% du temps.
Demande de 10 articles/période : 4% du temps.
Demande de 15 articles/période : 10% du temps.
Etc.

Si X est la demande moyenne, on aura :

99,73% des demandes qui seront situées dans un intervalle de X ±3𝜎
95,45% des demandes qui seront situées dans un intervalle de X ±2𝜎
68,27% des demandes qui seront situées dans un intervalle de X ±1𝜎

On peut également, à partir de tables de probabilités, déterminer le niveau du stock de sécurité pour obtenir un taux de service objectif.

Un stock de sécurité de un écart-type donnera un taux de service de :

𝜎 =

68,27 % / 2

+ 50 % = 84,135%

La loi normale

Lorsqu'un phénomène est influencé par plusieurs facteurs indépendants, les résultats des mesures de ce phénomène obéissent à une loi que l'on appelle la loi normale.

La loi normale décrit beaucoup de phénomènes naturels et peut être utilisée dans un grand nombre de situations.

Qu'est-ce qu'une distribution normale ?

La distribution normale est une distribution de probabilité continue, contrairement à la loi de Poisson ou à la loi binomiale qui sont des distributions de probabilité discrète.

On peut parler également de distribution Gaussienne. On notera que sa représentation graphique est appelée courbe en cloche. La courbe normale a la particularité d'être symétrique.

Quelle est la formule de la loi normale ?

La variable utilisée est continue, C'est-à-dire qu'elle peut prendre un nombre indéfini de valeurs.

Cette courbe a deux paramètres : μ et σ.

formule loi normale :

\begin{matrix} p (x) = \frac{1}{σ \sqrt 2 π} \exp (- \frac{(x - μ)^{2}}{2 σ^{2}}) \end{matrix}

avec :

μ : moyenne
σ : écart type
e : Le nombre d'Euler (2,71828)
π : Pi (3.14159)

N'ayez pas peur de cette formule puisque vous n'aurez pas à l'utiliser. En effet, les outils, tel que Excel, permettent de réaliser très facilement son calcul.

Loi normale centrée réduite

Astuce Excel pour calculer la probabilité

Il est possible d'utiliser la formule Excel suivante :

=LOI.NORMALE.STANDARD.N(Z;VRAI)-(1-LOI.NORMALE.STANDARD.N(Z;VRAI))

Par exemple, pour calculer la probabilité dans une aire comprise entre -1.8 α et +1.8 α on appliquera la formule en remplaçant Z par 1.8 :

=LOI.NORMALE.STANDARD.N(1.8;VRAI)-(1-LOI.NORMALE.STANDARD.N(1.8;VRAI))

Le résultat obtenu sera : 92.82%

Pourquoi utiliser le Z-score ?

Le principe est de convertir les valeurs de l'unité de mesure originale en une nouvelle unité appelé le Z-score (ou cote Z).

La cote Z correspond au nombre d'écarts types séparant un résultat de la moyenne.

Exemple d'une distribution quelconque centré sur μ et d'écart-type σ.

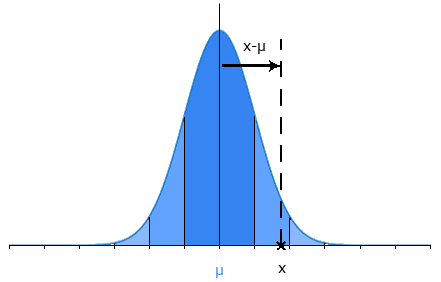
La formule est la suivante :

\begin{matrix} Z = \frac{x - μ}{σ} \end{matrix}

En d'autres termes, le Z score défini de combien d'écart-types la valeur recherchée est éloignée de la moyenne.

Ainsi, si on décale la distribution sur "0" en soustrayant la valeur de la moyenne μ, on obtient un écart-type égale à "1" en divisant par l'écart-type de la population.

Le Z-score correspondra ainsi à la coordonnée en abscisse. On n'aura plus à soustraire μ, car la moyenne sera de 0 et on n'aura pas à diviser par sigma σ car l'écart-type sera de 1.

Table de la loi normale centrée réduite

Comme il existe une infinité de loi normale, pour simplifier les choses, on choisi une loi normale spécifique de paramètres : μ=0 et de σ=1. Cette distribution est connue sous le nom de loi normale centrée réduite.

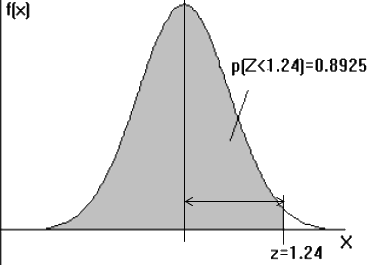
Interprétation de l'écart-type de la loi normale centrée réduite.

Les valeurs en abscisse représentent des unités d'écart-type.

Sur l'axes des abscisses on trouve des valeurs allant de -6σ à +6σ.

Le centre de la courbe est positionné au-dessus de 0.

Lecture de la table : Pour z=1.24 (intersection de la ligne 1.2 et de la colonne 0.04), on a la proportion P(Z < 1,24) = 0.8925

Z	0,00	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
0,0	0,5000	0,5040	0,5080	0,5120	0,5160	0,5199	0,5239	0,5279	0,5319	0,5359
0,1	0,5398	0,5438	0,5478	0,5517	0,5557	0,5596	0,5636	0,5675	0,5714	0,5753
0,2	0,5793	0,5832	0,5871	0,5910	0,5948	0,5987	0,6026	0,6064	0,6103	0,6141
0,3	0,6179	0,6217	0,6255	0,6293	0,6331	0,6368	0,6406	0,6443	0,6480	0,6517
0,4	0,6554	0,6591	0,6628	0,6664	0,6700	0,6736	0,6772	0,6808	0,6844	0,6879
0,5	0,6915	0,6950	0,6985	0,7019	0,7054	0,7088	0,7123	0,7157	0,7190	0,7224
0,6	0,7257	0,7291	0,7324	0,7357	0,7389	0,7422	0,7454	0,7486	0,7517	0,7549
0,7	0,7580	0,7611	0,7642	0,7673	0,7704	0,7734	0,7764	0,7794	0,7823	0,7852
0,8	0,7881	0,7910	0,7939	0,7967	0,7995	0,8023	0,8051	0,8078	0,8106	0,8133
0,9	0,8159	0,8186	0,8212	0,8238	0,8264	0,8289	0,8315	0,8340	0,8365	0,8389
1,0	0,8413	0,8438	0,8461	0,8485	0,8508	0,8531	0,8554	0,8577	0,8599	0,8621
1,1	0,8643	0,8665	0,8686	0,8708	0,8729	0,8749	0,8770	0,8790	0,8810	0,8830
1,2	0,8849	0,8869	0,8888	0,8907	0,8925	0,8944	0,8962	0,8980	0,8997	0,9015
1,3	0,9032	0,9049	0,9066	0,9082	0,9099	0,9115	0,9131	0,9147	0,9162	0,9177
1,4	0,9192	0,9207	0,9222	0,9236	0,9251	0,9265	0,9279	0,9292	0,9306	0,9319
1,5	0,9332	0,9345	0,9357	0,9370	0,9382	0,9394	0,9406	0,9418	0,9429	0,9441
1,6	0,9452	0,9463	0,9474	0,9484	0,9495	0,9505	0,9515	0,9525	0,9535	0,9545
1,7	0,9554	0,9564	0,9573	0,9582	0,9591	0,9599	0,9608	0,9616	0,9625	0,9633
1,8	0,9641	0,9649	0,9656	0,9664	0,9671	0,9678	0,9686	0,9693	0,9699	0,9706
1,9	0,9713	0,9719	0,9726	0,9732	0,9738	0,9744	0,9750	0,9756	0,9761	0,9767
2,0	0,9772	0,9778	0,9783	0,9788	0,9793	0,9798	0,9803	0,9808	0,9812	0,9817
2,1	0,9821	0,9826	0,9830	0,9834	0,9838	0,9842	0,9846	0,9850	0,9854	0,9857
2,2	0,9861	0,9864	0,9868	0,9871	0,9875	0,9878	0,9881	0,9884	0,9887	0,9890
2,3	0,9893	0,9896	0,9898	0,9901	0,9904	0,9906	0,9909	0,9911	0,9913	0,9916
2,4	0,9918	0,9920	0,9922	0,9925	0,9927	0,9929	0,9931	0,9932	0,9934	0,9936
2,5	0,9938	0,9940	0,9941	0,9943	0,9945	0,9946	0,9948	0,9949	0,9951	0,9952
2,6	0,9953	0,9955	0,9956	0,9957	0,9959	0,9960	0,9961	0,9962	0,9963	0,9964
2,7	0,9965	0,9966	0,9967	0,9968	0,9969	0,9970	0,9971	0,9972	0,9973	0,9974
2,8	0,9974	0,9975	0,9976	0,9977	0,9977	0,9978	0,9979	0,9979	0,9980	0,9981
2,9	0,9981	0,9982	0,9982	0,9983	0,9984	0,9984	0,9985	0,9985	0,9986	0,9986
3,0	0,9987	0,9987	0,9987	0,9988	0,9988	0,9989	0,9989	0,9989	0,9990	0,9990
3,1	0,9990	0,9991	0,9991	0,9991	0,9992	0,9992	0,9992	0,9992	0,9993	0,9993
3,2	0,9993	0,9993	0,9994	0,9994	0,9994	0,9994	0,9994	0,9995	0,9995	0,9995
3,3	0,9995	0,9995	0,9995	0,9996	0,9996	0,9996	0,9996	0,9996	0,9996	0,9997
3,4	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9998
3,5	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998

Calcul du stock de sécurité

Exercice : calculer le stock de sécurité permettant d'avoir « x% » de chance de ne jamais être en rupture de stock. La demande n'est pas constante, mais aléatoire et, de plus, les délais de livraison ou de fabrication peuvent eux-mêmes être aléatoires !

Délai de livraison fixe

Considérons un laps de temps comprenant un assez grand nombre de périodes, et faisons les hypothèses suivantes :

Le délai de livraison D est fixe.
La consommation varie autour d'une moyenne sur une période x et selon une loi normale d'écart type 𝜎_x
Sur le laps de temps T, on considère que les périodes sont indépendantes.

Il y a donc additivité des variances : 𝜎²_x,D = D * 𝜎²_x

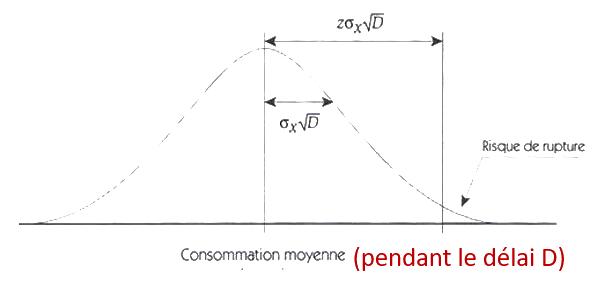
La consommation sur une période D suit donc une loi normale d'écart type 𝜎_x,D = 𝜎_x * √D

Le stock de sécurité est donc égal à :

SS = z * 𝜎_x * √D

Z étant la variable réduite associée au risque de rupture choisi.

On note tout de suite l'intérêt fondamental qu'il y a à réduire de façon considérable le délai de fabrication ou de livraison afin de pouvoir diminuer le stock de sécurité.

Consommation fixe :

Soit 𝜎_d (jours), l'écart type de la variation sur le délai de livraison.

Effectuons un changement de variables jour → consommation :

𝜎_d(Conso) = (Consommation/jour) . 𝜎_d (jours)

Le stock de sécurité est donc égal à :

SS = z * 𝜎_d

z étant la variable réduite associée au risque de rupture choisi.

Consommation et délai variables

Le délai et la consommation étant des variables indépendantes, on peut appliquer le théorème d'additivité des variances.

𝜎² = 𝜎²_d + D * 𝜎²_x

Le stock de sécurité est donc égal à :

SS = z * 𝜎 = z * √𝜎²_d + D * 𝜎²_x

z étant la variable réduite associée au risque de rupture choisi.

Exercice 1

Un article de consommation suit une loi de Gauss de moyenne hebdomadaire X = 50 unités et d'écart-type de : 𝜎_x = 5 unités.

Le délai moyen de livraison est de 4 semaines (20 jours) avec une variation d'écart type de deux jours : 𝜎_d = 2.

En considérant le délai fixe, on peut calculer : 𝜎²_x,D = D * 𝜎²_x = 4 * 5² = 100

En considérant la consommation fixe, on peut calculer :

𝜎_d(conso) = (Consommation/jour) * 𝜎_d (jours) = 10 * 2 = 20 , soit 𝜎²_l = 400

En considérant la consommation et le délai variables, on peut calculer :

𝜎² = 𝜎²_d + D * 𝜎²_x = 400 + 100 = 500 , soit 𝜎 = 22.36

En acceptant un risque de rupture de 2,5% (taux de service = 97,5%), le stock de sécurité sera :

D'après table de loi normale réduite z = 1.96

SS = z * 𝜎 = 1.96 * 22.36 = 44 pièces

Exercice 2

Qté de commande = 2 600 pièces
Délai = 1 mois (4 semaines)
1 commande/an en retard acceptée (52 semaines)

Calculer :

Nombre de commandes/an
Taux de service visé
Stock de sécurité
Point de commande

Demande actuelle :

Semaine	Pièces
1	1200
2	1000
3	800
4	900
5	1400
6	1100
7	1100
8	700
9	1000
10	800

Corrigé

Semaine	Pièces	X-X	(X-X)²
1	1 200	200	40 000
2	1000	0	0
3	800	-200	40 000
4	900	-100	10 000
5	1 400	400	160 000
6	1 100	100	10 000
7	1 100	100	10 000
8	700	-300	90 000
9	1 000	0	0
10	800	-200	40 000
Total	10 000		400 000

X =

10 000 / 10

= 1000

𝜎 = √

400 000 / 9

= 211 pièces

Nombre de commandes / an :

Demande annuelle =
10 000 / 10
* 52 = 52 000 pièces
Nombre de commande/an =
52 000 / 2 600
= 20

Taux de service

1 commande en retard /an
Taux de service =
(20 – 1) / 20
= 95 %

Stock de sécurité

95 % pour 1,65 σ (z = 1,65)
Stock de sécurité = 1,65 * 211 * √4 = 696

Point de commande

Demande pendant le délai =
10 000 / 10
* 4 = 4 000 pièces
Point de commande = 4 000 + 696 = 4 696 pièces

Cas d'emploi d'un stock de sécurité fixe

Lancement d'un nouveau produit.
Fin de vie d'un produit.
Articles à demande dépendante, consommés et planifiés avec le MRP.

Pas d'historique ou de prévision de consommation stable et fiable : donc selon le gestionnaire.
Mise à 0 sinon non consommation du stock de sécurité.
Stock de sécurité fixe et à zéro.