Introduction au concept FMD : Fiabilité - Maintenabilité - Disponibilité
Définitions
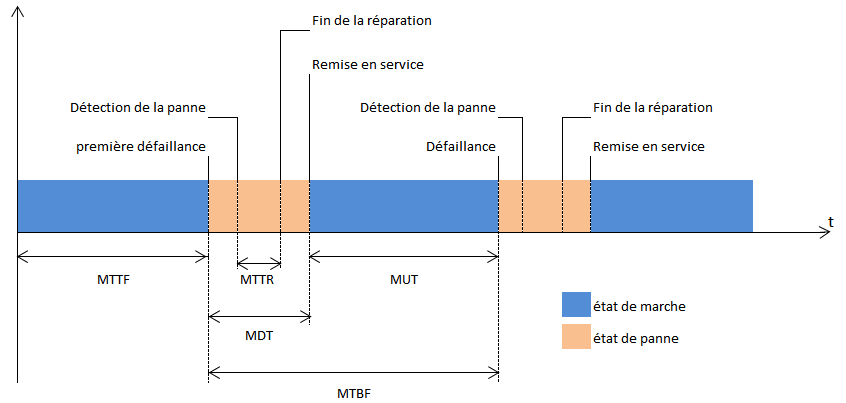
- MTTF - Mean Time To Failure
- Durée moyenne de fonctionnement d'une entité avant la première défaillance MTTF = ∫ [0;+∞[ R(x).dx
- MTTR - Mean Time To Repair
- Durée moyenne de réparation
- MUT - Mean Up Time
- Durée moyenne de fonctionnement après réparation
- MDT - Mean Down Time
- Durée moyenne d'indisponibilité (temps de détection de la panne + temps de réparation + temps de remise en service)
- MTBF - Mean Time Between Failure
- Durée moyenne des temps de bon fonctionnement entre deux défaillances consécutives
Remarques :
- La somme des temps de bon fonctionnement est égale au temps total d'analyse (période de référence) moins la somme des temps d'arrêts
- Le nombre de périodes de bon fonctionnement (tbf) est normalement égal au nombre de défaillances (arrêts) de la période si on considère le début et la fin de la période comme un seul temps de bon fonctionnement (Cas n°1) ou bien si on effectue l'analyse entre deux arrêts, sans prendre en compte l'arrêt initial (Cas n°2)
cas n°1 :
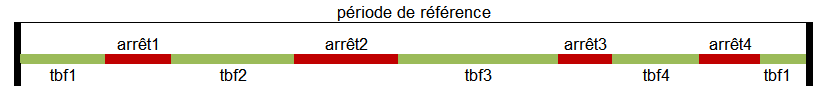
cas n°2 :

Maintenabilité
« Dans les conditions d'utilisation données pour lesquelles il a été conçu, la maintenabilité est l'aptitude d'un bien à être maintenu ou rétabli dans un état dans lequel il peut accomplir une fonction requise, lorsque la maintenance est accomplie dans des conditions données, avec des procédures et des moyens prescrits. »
(NF X60-010).
La maintenabilité caractérise la facilité à remettre ou de maintenir un bien en bon état de fonctionnement. Cette notion ne peut s'appliquer qu'à du matériel maintenable, donc réparable.
« Les moyens prescrits » englobent des notions très diverses : moyens en personnel, appareillages, outillages, etc.
La maintenabilité d'un équipement dépend de nombreux facteurs :
| ÉQUIPEMENT | CONSTRUCTEUR | MAINTENANCE |
|---|---|---|
| - documentation - aptitude au démontage - facilité d'utilisation |
- conception - qualité du service après-vente - facilité d'obtention des pièces de rechange - coût des pièces de rechange |
- préparation et formation des personnels - moyens adéquats - études d'améliorations (maintenance améliorative) |
Calcul de la maintenabilité
La maintenabilité concerne l'action de maintenance comme telle. Par la maintenabilité, on recherche l'optimisation du temps d'intervention afin d'augmenter le temps de production en diminuant les délais dûs au :
- temps pour l'attente de pièce de remplacement
- temps pour compléter les documents
- temps de préparation de l'action
Son indice est le MTTR et se calcule de manière suivante :
La maintenabilité peut se caractériser par sa MTTR (Mean Time To Repair) ou encore Moyenne des Temps Techniques de Réparation
Pour l'exemple traité en fiabilité :
Taux de réparation μ
Il est égal à l'unité de temps sur la MTTR :
Fiabilité
Fiabilité (en anglais Reliability)
La fiabilité est la probabilité qu'un produit fonctionne correctement sans panne dans des conditions d'utilisation données pendant une durée spécifique.
"caractéristique d'un bien exprimée par la probabilité qu'il accomplisse une fonction requise dans des conditions données pendant un temps donné" (NF X50 –500).
Il s'agit d'une probabilité, notée R(t).
R(t) = probabilité que l'entité ne soit pas défaillante dans l'intervalle de temps [0;t]
Cette définition suppose que soit bien définis :
- Les conditions d'utilisation ;
- Le temps moyen souhaité entre les pannes.
L'indice de fiabilité le plus employé est le MTBF
Défiabilité
A l'inverse de la fiabilité, la défiabilité est la probabilité que l'entité ait connu une défaillance pendant une durée donnée.
Elle est notée F(t)
F(t) = probabilité que l'entité soit défaillante dans l'intervalle de temps [0;t]
F(t) = 1-R(t)
La notion de temps peut prendre la forme :
- De nombre de cycles effectués => machine automatique
- De distance parcourue => matériel roulant
- De tonnage produit => équipement de production
Un équipement est fiable s'il subit peu d'arrêts pour pannes. La notion de fiabilité s'applique :
- à du système réparable => équipement industriel ou domestique.
- à des systèmes non réparables => lampes, composants donc jetables
Calcul de la MTBF
La fiabilité peut se caractériser par la moyenne des temps de bon fonctionnement ou MTBF (Mean Time Between Failure).
Il se calcule ainsi :
si le MTBF est calculé suite à un TBF
si le MTBF est calculé suite à un TA
Exemple :
Fonctionnement d'un équipement sur 24 heures
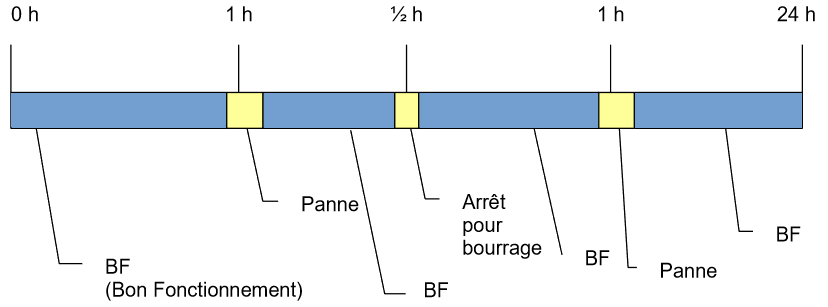
Taux de défaillance λ
Le taux de défaillance instantané est le taux de défaillance d'un système ayant fonctionné pendant une durée t.
Appelé également taux de panne, il est égal à l'unité de temps sur la MTBF :
Pour l'exemple précédent :
Pour un équipement (système réparable) le taux de défaillance se traduit souvent par une courbe dite « courbe en baignoire » mettant en évidence 3 époques :
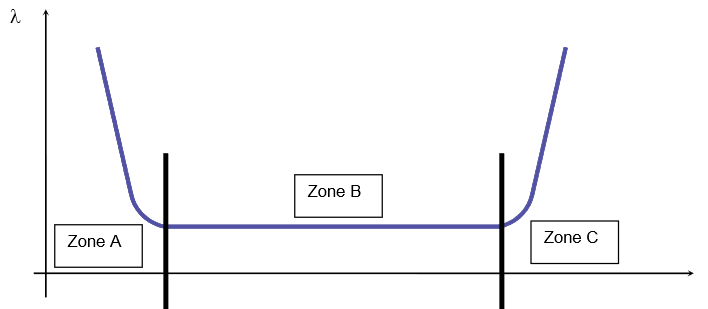
- Zone A => époque de jeunesse
- Zone B => époque de maturité, fonctionnement normal, défaillance aléatoire indépendante du temps
- Zone C => époque d'obsolescence, défaillances d'usure ou pannes de vieillesse
Exemple :
Dans cette partie, on s'intéresse au temps de bon fonctionnement (TBF) d'une presse. A chaque panne, on associe le nombre de jours de bon fonctionnement ayant précédé de cette panne.
Les observations se sont déroulées sur une période de 4 ans et ont donné les résultats suivants :
| Rang de la panne | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| TBF ayant précédé la panne (en jour) | 55 | 26 | 13 | 80 | 14 | 21 | 124 | 35 | 18 | 26 |
Calculer au jour près par défaut, le temps moyen de bon fonctionnement entre deux pannes.
Fiabilité des systèmes
Lorsque les équipements sont composés de plusieurs équipements formant ainsi un système, il faut ajuster le calcul de la fiabilité au système.
De façon générale, les systèmes sont en série ou en parallèle.
Système en série
Un système constitué de n éléments est dit en série si la défaillance d'un élément entraîne celle du système et si les défaillances sont indépendantes.
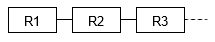
La fiabilité résultante est donnée par :
R(t) = π Ri(t)
i=1
La fiabilité du système en série se calcul ainsi :
R(t) = R1(t) x R2(t) x R3(t) x … Rn(t)
Système en parallèle
Un système est dit en parallèle s'il suffit qu'un seul des élément fonctionne pour que le système fonctionne.
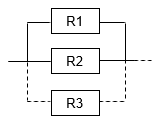
La fiabilité résultante est donnée par :
R(t) = 1 - π (1 - Ri(t))
i=1
La fiabilité du système en série se calcule ainsi :
R(t) = 1-( (1-R1(t)) x (1-R2(t)) x … x (1-Rn(t)) )
Remarque :
Plus il y a de composantes en parallèle, meilleure est la fiabilité.
Habituellement, on utilise cette propriété pour accroître la sécurité de fonctionnement d'un système.
Exemple :
- système de freins d'urgence sur une automobile
- deux pompes en parallèle
Exercices
MTBF est l'abréviation pour Temps Moyen de Bon Fonctionnement (Mean Time Between Failures en anglais). Le MTBF est un indicateur de la fiabilité d'un produit ou d'un système réparable. Il mesure le taux de défaillances aléatoires à l'exclusion des pannes systématiques dues par exemple aux erreurs de conception (par exemple erreurs logiciel) ou défauts de fabrication (produits en début de vie) et à l'exclusion de l'usure due à l'usage (fin de vie d'un produit).
Le MTBF s'exprime habituellement en nombre d'heures. Plus le MTBF est élevé, plus le produit ou le système est fiable.
La valeur du MTBF ne peut être définie que pour un usage et un environnement donnés. Par exemple, le MTBF d'un produit donné pour fonctionner entre -20°C et +70°C sera différent selon que le produit est utilisé en intérieur à 20°C ou en extérieur à 70°C.
Calculs de MTBF
Lorsqu'un système est composé de plusieurs composants, on fait la somme des défaillances de chaque composant en supposant que la panne d'un seul composant provoque la panne du système.
Note : Ceci ne s'applique pas aux systèmes complexes (par exemple système redondant) où les taux de défaillances ne sont plus constants.
La probabilité (P) que le produit fonctionnera pendant un temps T avant une panne est égale à :
Exemple 1 : Centrale OLDHAM MX 43, version 4 voies, alimentation 24 V, température d'utilisation 25°C
MTBF = 174805 heures ( ?? ans)
La probabilité que la centrale fonctionne 5 ans avant de tomber en panne est de P = ?? %.
Exemple 2 : Détecteur de gaz OLDHAM OLCT 100 pour la détection des gaz explosibles.
Ce détecteur a été certifié SIL2 par un organisme certifié. Les données de fiabilité sont les suivantes :
- Taux de défaillances dangereuses non détectées (λdu) = 189.10-9 par heure
- Proportion de défaillances non dangereuses (SFF) = 92,9%
donc Σ des taux de défaillance = 2,66.10-6 par heure = ?? par an
et
La probabilité que le détecteur fonctionne 4 ans (durée de vie moyenne d'une cellule de détection pour les gaz explosibles) avant de tomber en panne est de : ? %.
En fait le MTBF intègre également le temps nécessaire au diagnostic de la panne, à l'approvisionnement des pièces détachées et à la remise en état de fonctionnement (la somme de ces temps correspond au MTTR : temps moyen avant réparation ou Mean Time To Repair en anglais).
Dans le cas de l'OLCT100 le MTTR est de ?? heures et reste négligeable devant ?? ans.
Disponibilité
« Aptitude d'un bien, sous les aspects combinés de sa fiabilité, de sa maintenabilité et de l'organisation de la maintenance, à être en état d'accomplir une fonction requise dans des conditions de temps déterminées »
(NF X60-010)
Pour qu'un équipement présente une bonne disponibilité, il doit :
- Avoir le moins possible d'arrêts de production
- Être rapidement remis en bon état s'il tombe en panne
La disponibilité d'un équipement dépend de nombreux facteurs :
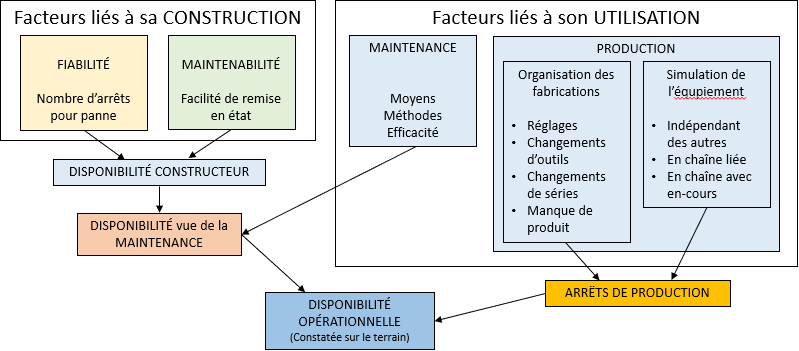
La disponibilité allie donc les notions de fiabilité et de maintenabilité
Augmenter la disponibilité passe par :
- L'allongement de la MTBF (action sur la fiabilité)
- La réduction de la MTTR (action sur la maintenance)
Synthèse
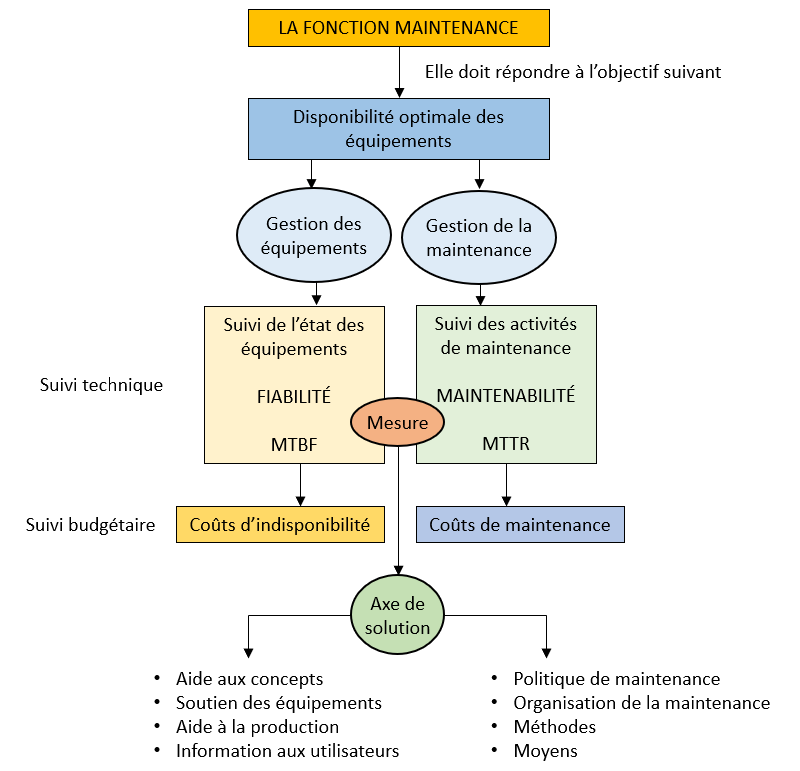
La disponibilité est un indice qui est en général mesuré car il inclut les précédents.
Il détermine la disponibilité d'un équipement à effectuer son travail dans le temps.
On le calcule ainsi :