Méthodes d'implantation
1. Méthodes des ficelles
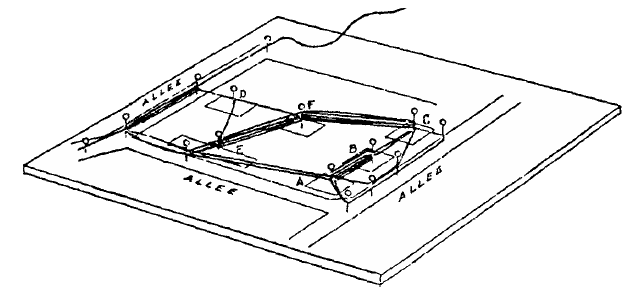
Cette méthode est surtout pratique pour estimer l'ampleur des flux et des circulations.
On tend sur un plan des fils de couleurs correspondant aux transports à effectuer : la densité de la nappe de fils renseigne sur les débits à assurer et l'importance à donner aux aires de circulation.
Cette méthode conçue initialement avec des ficelles peut facilement être transposable sous forme informatique.
Un tel diagramme permet de déterminer :
- La longueur des flux.
- Les passages fréquentés.
- Les cheminements difficiles.
- Les emplacements peu accessibles.
- Les goulots d'étranglement.
- Les points d'attente.
2. Méthodes des chaînons
Objectif :
Organiser l'implantation d'une unité de production, en structurant et raccourcissant le flux de matières.
Méthodologie :
- Inventorier les postes de travail et les gammes opératoires.
- Appliquer la méthode des chaînons.
- Tracer l'implantation théorique.
- Adapter l'implantation théorique dans les locaux prévus.
Définitions :
- Chaînon
- Trajectoire de manutention réunissant les postes de travail successifs.
- Noeud
- Poste de travail d'où émanent un ou plusieurs chaînons.
La démarche comprend 5 phases :
- Définir la table des chaînons.
- Déterminer les indices de flux.
- Déterminer le nombre de chaînons de chaque poste.
- Tracer l'implantation théorique.
- Adapter l'implantation théorique aux locaux..
Exemple :
Atelier de 6 postes de production (M1 à M6) permettant la réalisation de 5 produits (P1 à P5).
Le nombre de transferts peut être défini par le nombre de lots de transfert moyen durant une équipe de production.
| Produits | Gamme / Phases | Nb de transferts | ||||
|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | ||
| P1 | M1 | M4 | M2 | M5 | 25 | |
| P2 | M6 | M2 | M4 | M1 | M2 | 43 |
| P3 | M6 | M2 | M4 | M1 | 15 | |
| P4 | M1 | M3 | M2 | 24 | ||
| P5 | M1 | M2 | M3 | M4 | 90 | |
Phase 1 : Définir la table des chaînons.
La table des chaînons se présente sous la forme d'une demi-matrice dont les lignes et les colonnes désignent les différents postes de travail.
Chaque case de la matrice représente un chaînon, c'est-à-dire un flux de pièces entre les deux postes (indépendamment du sens de déplacement).
| M1 | |||||
| X | M2 | ||||
| M3 | |||||
| M4 | |||||
| M5 | |||||
| M6 |
X représente le flux de transfert entre M2 et M4 ou entre M4 et M2.
Phase 2 : Déterminer les indices de flux.
Pour déterminer les indices de flux, il faut, pour chaque gamme, inscrire dans les cases correspondantes le nombre de transferts.
Ainsi, pour le produit P1, la gamme est : M1, M4, M2, M5.
Les chaînons concernés sont donc M1M4, M4M2 et M2M5. Le nombre de transferts est de 25.
La matrice devient :
| 25 | M1 | ||||
| 25 | 25 | M2 | |||
| M3 | |||||
| M4 | |||||
| M5 | |||||
| M6 |
On réalise la même démarche en ajoutant le nombre de transferts à chaque maillon concerné par la gamme d'un produit.
| 83 | 24 | 133 | M1 | ||
| 58 | 25 | 83 | 114 | M2 | |
| 90 | M3 | ||||
| M4 | |||||
| M5 | |||||
| M6 |
Phase 3 : Déterminer le nombre de chaînons de chaque poste.
Cela revient à calculer le nombre de maillons partant ou arrivant à un poste.
Pour cela, il suffit de compter le nombre de cases remplies sur la ligne et sur la colonne de chaque poste.
Le schéma peut être complété par un classement par ordre d'importance.
| 83 | 24 | 133 | M1 | |||
| 58 | 25 | 83 | 114 | M2 | 3 2e | |
| 90 | M3 | 5 1er | ||||
| M4 | 3 2e | |||||
| M5 | 3 2e | |||||
| M6 | 1 5e | |||||
| 1 5e |
Autre représentation
| M1 | M2 | M3 | M4 | M5 | M6 | |
| M6 | ||||||
| M5 | ||||||
| M4 | X | |||||
| M3 | ||||||
| M2 | ||||||
| M1 |
| Indice total de flux arrivant au poste M2 = ∑ indices de flux des colonnes et des lignes. | |
| Nombres de chaînons aboutissants au poste M5. |
X représente le flux de transfert entre M3 et M4.
Ce qui donnerait pour l'exemple précédent :
| |
M1 | M2 | M3 | M4 | M5 | M6 | |
| M6 | 43 15 |
58 1 |
|||||
| M5 | 25 |
25 1 |
5e | ||||
| M4 | 25 15 43 |
25 15 43 |
90 | 256 3 |
6e | ||
| M3 | 24 |
24 90 |
228 3 |
2e | |||
| M2 | 43 90 |
413 5 |
4e | ||||
| M1 | 240 3 |
1er | |||||
| |
3e |
Phase 4 : Tracer l'implantation théorique.
Choisir le poste le plus chargé (M2 dans notre exemple) et le placer sur un nœud de la trame.
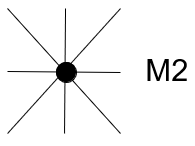
Choisir le poste non placé le plus chargé.
Dans notre exemple, prenons M1 et le placer sur un nœud.
Le maillon M1M2 existe, nous choisissons un nœud proche de M2.
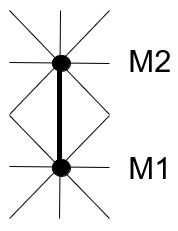
Nous continuons sur le même principe en plaçant M4.
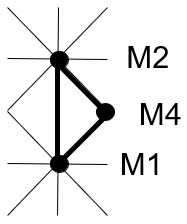
Puis M3.
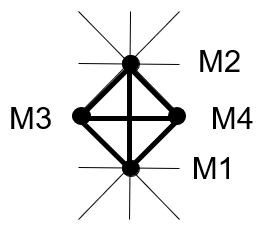
Enfin nous plaçons les postes M5 et M6 ayant le plus faible nombre de maillons .
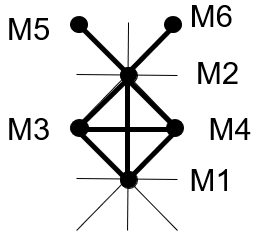
Cette solution fait apparaître un croisement de flux entre M2M1 et M3M4. Les indices de circulation de ces maillons étant 133 et 90 le premier et le troisième en importance, cette solution n'est pas satisfaisante.
Lors de la deuxième itération, nous avions le choix de placer 3 postes de même poids (M1, M3, M4), regardons les autres solutions.
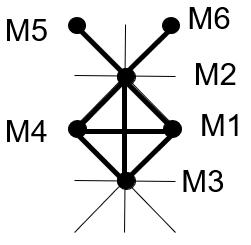
Dans le premier cas nous avons un croisement entre M2M3 (114) et M1M4 (83).
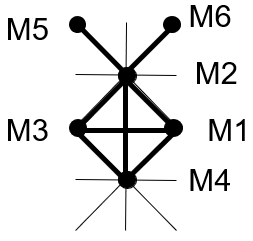
Dans le second cas nous avons un croisement entre M2M4 (83) et M1M3 (24).
Cette dernière solution aura donc notre préférence.
Phase 5 : Adapter l'implantation théorique aux locaux.
Pour cela, il faut tenir compte de la forme des bâtiments, de l'emplacement des entrées sorties possibles, de l'emplacements des poteaux et de la forme des équipements.
Identification des entrées sorties de matière.
Sur l'ensemble des gammes, il existe 2 postes d'entrée M1 et M6 et 4 postes de sortie M1, M2, M4 et M5.
L'étude d'implantation peut être réalisée soit, en utilisant un logiciel de dessin, soit à partir de silhouettes et d'un plan des bâtiments.
Autre exemple :
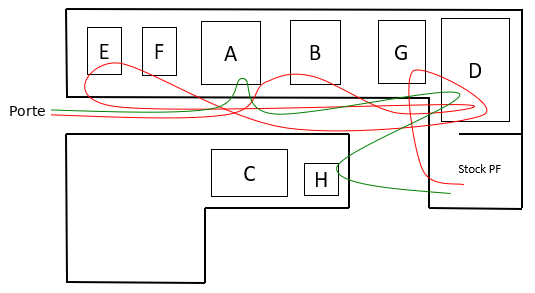
Contraintes :
Le poste D; machine à laver ne peut être déplacé à cause de l'alimentation en eau et l'évacuation.
| Produits | Gammes | Programme de production | ||||
|---|---|---|---|---|---|---|
| Référence | Nom | Produit | Gamme | Quantité | Pièces/ Panier |
Nb paniers |
| A | Tour n°1 | P1 | A - B - D - E - D - G | 20 000 | 100 | 200 |
| B | Tour n°2 | P2 | A - D - H | 25 000 | 250 | 100 |
| C | Tronçonneuse | P3 | C - B - E | 12 500 | 100 | 125 |
| D | Machine à laver | P4 | C - B - F - D - H | 5 000 | 10 | 500 |
| E | Reprise 1 | P5 | A - D - H | 35 000 | 500 | 70 |
| F | Reprise 2 | |||||
| G | Rectifieuse 1 | |||||
| H | Rectifieuse 2 | |||||
La dernière colonne représente l'indice de traffic.
Détermination du nombre de chaînons.
| 100 500 70 |
H | |||||||
| 200 | G | |
1 6e | |||||
| 500 | 500 | F | |
1 6e | ||||
| 125 | 400 | E | |
2 3e | ||||
| 100 70 |
200 | D | |
2 3e | ||||
| 500 125 |
C | |
6 1er | |||||
| 200 | B | |
1 6e | |||||
| A | |
5 2e | ||||||
| |
2 3e |
Ou avec la deuxième représentation :
| |
A | B | C | D | E | F | G | H | |
| H | 100 500 70 |
670 1 |
|||||||
| G | 200 |
200 1 |
6e | ||||||
| F | 500 | 500 | 1000 2 |
8e | |||||
| E | 125 |
400 | 525 2 |
3e | |||||
| D | 100 70 |
200 | 2140 6 |
4e | |||||
| C | 500 125 |
625 1 |
1er | ||||||
| B | 200 | 1650 5 |
7e | ||||||
| A | 370 2 |
|
2e | ||||||
| |
5e |
Résultat de l'implantation
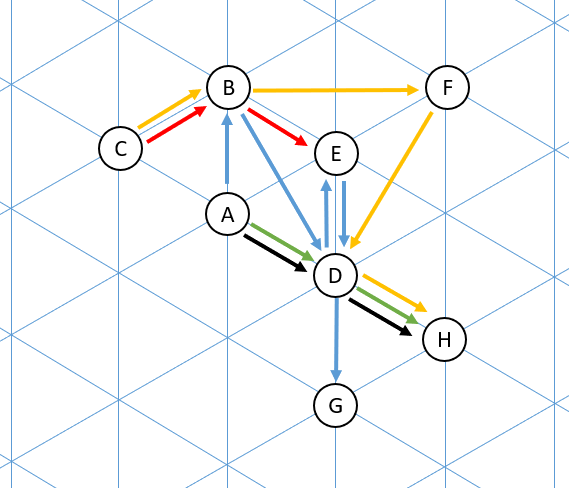
La machine B devrait être placée au plus près de la machine D selon l'ordre du classement trouvé précédemment.
Mais cela engendrerait un croisement de flux. En déplaçant cette machine un peu plus loin, on arrive à faire en sorte qu'il n'y ait plus de croisement de flux.