Méthodes d'estimation de la demande
Avant-propos
Une prévision est toujours fausse ! L'objectif est de réduire l'incertitude par l'utilisation de méthodes.
… Qui veut bien juger de l'avenir doit consulter les temps passés …
Jacques-Bénigne Bossuet
Les méthodes reposent sur 2 postulats :
- « L'avenir est contenu dans le passé… »
- « La nature ne fait pas de saut… »
Le cycle de vie du produit
Les gestions de la demande d'un produit n'est pas la même en fonction du cycle de vie du produit.
L'innovation accrue et les délais réduits de mise sur le marché des nouveaux produits rendent le travail des prévisions compliqué.
On distingue 3 phases :
- Phase de lancement relativement lente.
- Phase de croissance rapide.
- Phase de saturation du marché et de légère décroissance.
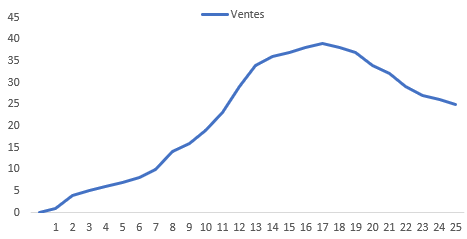
Remarque :
Être vigilant lors du passage d'une phase à une autre !
Introduire la notion de cycle de vie dans la segmentation des produits.
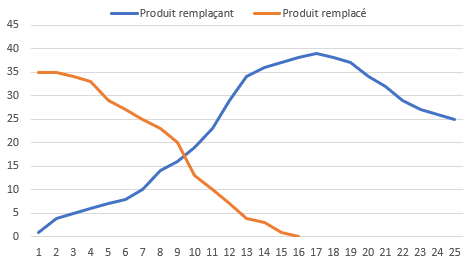
Les biseaux
Le problème se complique lorsqu'un produit est remplacé par un nouveau.
Avec des cycles de mise en marché des nouveaux produits plus courts, nous avons de plus en plus de biseaux à gérer !
Il s'agit dès lors d'organiser l'épuisement du stock du produit remplacé, avant de commencer à distribuer le nouveau (revente des produits en fin de vie à des brokers, boutique d'usine, …).
Cela en travaillant en collaboration avec le marketing, la production et l'ingénierie afin de bien préparer la fin de vie du produit remplacé.
Les étapes d'une prévision
- Préciser le but de la prévision.
- Déterminer l'horizon de temps.
- Choisir une méthode de prévision.
- Recueillir des données pertinentes des sources fiables.
- Établir un modèle de prévision.
- Évaluer le modèle.
- Implanter les résultats du modèle.
- Entretenir le modèle de prévision.
Séries chronologiques.
Une série chronologique est un ensemble d'observations faites à des moments précis, généralement à intervalles réguliers dans le temps.
Séries chronologiques : les composantes.
- La tendance (a).
- Le niveau ou une valeur moyenne (b).
- La variation saisonnière (Ft).
- La variation cyclique (Ct).
- La variation irrégulière ou composante aléatoire (εt).
Forme des séries chronologiques.
En général
yt = f(a, b, Ft, Ct, εt)
Modèle additif
yt = a.t + b + Ft + Ct + εt
Modèle multiplicatif
yt = (a.t + b).Ft.Ct.εt
Modèle mixte
yt = (a.t + b).Ft + Ct + εt
Modèles de prévision simples.
Ce sont des méthodes basées sur la moyenne ou la moyenne mobile.
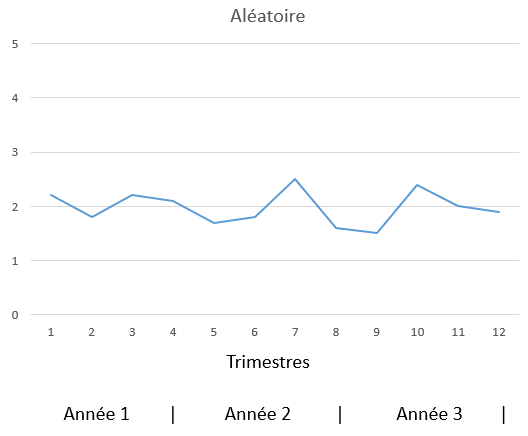
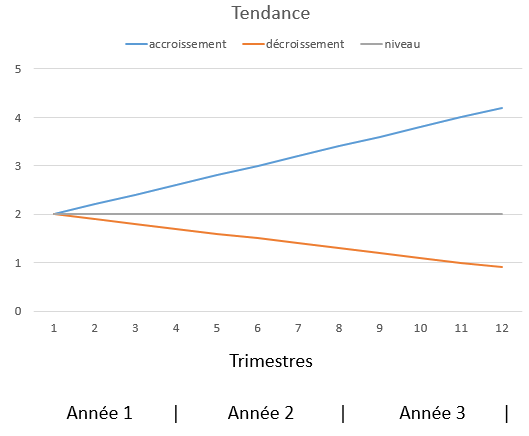
Utilisé quand :
- la demande est stable, c'est-à-dire, il existe des variations autour d'un niveau moyen constant,
- il n'y a quasiment pas de tendance ni de saisonnalité,
- et les variations sont aléatoires.
Quand les demandes passées montrent des variations aléatoires :
- Ne devinez pas quels seront les effets.
- Utilisez les prévisions en fonction de la demande moyenne.
Moyenne simple.
Exemple :
| Jan | Fév | Mars | Avr | Mai | Juin | Juil | Août | Sep | Oct | Nov | Déc | Jan |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 74 | 66 | 47 | 56 | 57 | 66 | 65 | 63 | 57 | 44 | 70 | 67 | ? |
Prévision janvier précédent : 74
Prévision mois précédent : 67
Moyenne : 61
La variation est aléatoire, et il n'existe pas de tendance à la hausse ou à la baisse et la somme des variations = 0 Il es préférable d'utiliser la moyenne 61 ! Ça neutralise l'impact de la variation aléatoire et la prévision est plus sûre.
Valeurs de la prévision
Historique de consommation Produit A, et B / Semaine.
| Semaine | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | Moyenne |
|---|---|---|---|---|---|---|---|---|---|---|
| Produit A | 300 | 200 | 0 | 5 | 75 | 290 | 30 | 0 | 0 | ? |
| Produit B | 103 | 104 | 95 | 101 | 96 | 98 | 101 | 110 | 92 | ? |
1. Quelle prévision pour la semaine S10 pour le produit A et B ?
2. Quel est le point commun de ces deux séries ?
Réponses :
Les produits ont une moyenne identique, mais correspondent à des consommations très différentes.
Les consommations hebdomadaires passées peuvent s'analyser avec une moyenne
Mais la situation peut être différente selon la variabilité des consommations autour de cette moyenne.
Remarques :
La moyenne des consommations passées ne suffit pas et ne peut donc constituer une prévision.
Il faut ajouter d'autres éléments comme la dispersion, que l'on peut aussi appeler la fiabilité de la prévision.
Moyenne mobile = Demande moyenne de périodes passées.
Dans le cas d'une moyenne mobile, la prévision est obtenue en tenant compte des observations passées les plus pertinentes.
On utilise la moyenne mobile lorsque le niveau moyen de la demande varie dans le temps. (Il n'y a toujours pas de tendance ni de saisonnalité.
| Mois | Demande | Total Tri | Prévision |
|---|---|---|---|
| 1 | 85 | ||
| 2 | 78 | ||
| 3 | 80 | 243 | |
| 4 | 81 |
Ou plus globalement
Exemple :
Soit les données suivantes :
| Mois | Demande |
|---|---|
| 1 | 70 |
| 2 | 71 |
| 3 | 75 |
| 4 | 73 |
| 5 | 78 |
| 6 | 85 |
| 7 | 87 |
| 8 | 91 |
La prévision d'ordre 3 sera donc de :
P9 =
Ou, si on veut faire ça avec un tableur, la prévision à partir de la moyenne mobile sur trois mois.
| Mois | Demande | Total Tri | Prévision |
|---|---|---|---|
| 1 | 70 | ||
| 2 | 71 | ||
| 3 | 75 | 216 | |
| 4 | 73 | 219 | 72 |
| 5 | 78 | 226 | 73 |
| 6 | 85 | 236 | 75 |
| 7 | 87 | 250 | 79 |
| 8 | 91 | 263 | 83 |
| 9 | 88 |
Exemple : prévision à partir de la moyenne mobile sur six mois.
| Mois | Demande | Total Tri | Prévision |
|---|---|---|---|
| 1 | 70 | ||
| 2 | 71 | ||
| 3 | 75 | ||
| 4 | 73 | ||
| 5 | 78 | ||
| 6 | 85 | 435 | |
| 7 | 87 | 452 | 73 |
| 8 | 91 | 472 | 75 |
| 9 | 79 |
Moyenne mobile : ce qu'il faut retenir
- Retarde le développement de la tendance.
- Plus la prévision atteint tardivement les données plus le décalage est important.
- La prévision moyenne mobile sur 3 mois pourrait avoir réagi de manière excessive si l'évolution de la demande avait diminué.
- L'effet de lissage augmente quand le nombre de mois pris en compte augmente.
- La prévision moyenne mobile fonctionne le mieux quand la demande est stable avec des variations aléatoires ; elle filtre les variations aléatoires.
Limites du modèle
Cette méthode s'applique surtout dans les cas suivants :
- On fait de la prévision à court terme.
- Les fluctuations sont généralement peu importantes à court terme.
- Une certaine loi se dissimule dans les valeurs observées, affectée de fluctuation aléatoires.
- On veut prévoir une seule période.
Cette méthode s'adapte difficilement s'il y a apparition d'une tendance, d'une saisonnalité ou d'un cycle.
Cependant, dans les situations de « court terme », le modèle de prévision peut souvent être considérée comme horizontal (loi aléatoire variant autour d'une moyenne), sans qu'on ne perde trop de précision.
Lissage des prévisions
Moyenne mobile pondérée
On applique une pondération aux observations de façon à refléter leur pertinence.
Avec n = ordre de la moyenne mobile pondérée
𝛼i = poids accordé aux n dernières demandes
t = période pour laquelle on fait la prévision
Cela permet de moduler l'importance accordée aux diverses demandes.
Il n'y a toujours pas de tendance ni de variation saisonnière.
La somme des n coefficients 𝛼 doit évidemment être égal à 1.
Reprenons l'exemple précédent :
| Mois | Demande |
|---|---|
| 1 | 70 |
| 2 | 71 |
| 3 | 75 |
| 4 | 73 |
| 5 | 78 |
| 6 | 85 |
| 7 | 87 |
| 8 | 91 |
Avec comme coefficents de pondération : 𝛼1=0,5; 𝛼2=0,3; 𝛼3=0,2
La moyenne mobile d'ordre 3 sera donc de :
P9 = 3 Σ i=1 𝛼i 𝑥9−𝑖 = 𝛼1 * 𝑥8 + 𝛼2 * 𝑥7 + 𝛼3 * 𝑥6 = 0.5 * 91 + 0.3 * 87 + 0.2 * 85 = 88,6 donc 89Prévision saisonnière
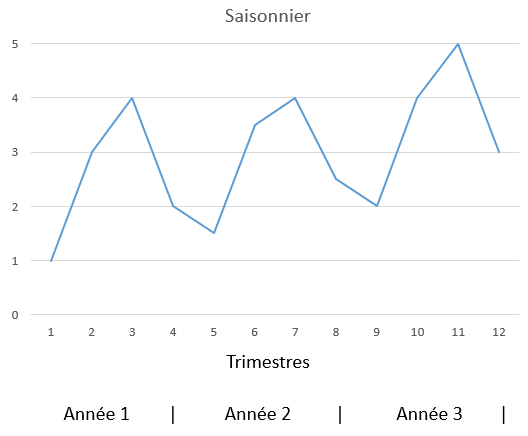
Les coefficients saisonniers permettent de mesurer l'importance de la composante saisonnière, en indiquant le poids d'activité de la période considérée (un mois ou un trimestre) par rapport à une activité moyenne ou globale.
En cas de saisonnalité, la procédure de prévision est la suivante :
- Calculer un index de saisonnalité de la demande pour chaque période pour établir la saisonnalité.
- Développer une prévision désaisonnalisée couvrant toutes les périodes.
- Développer une prévision saisonnalisée pour chaque période.
Deux méthodes existent pour les calculer : la méthode des coefficients simples et la méthode des coefficients moyens.
Saisonnalité avec les coefficients saisonniers simples
Le coefficient saisonnier simple s'obtient par le rapport entre chaque période et le total général.
Exemple :
Étape 1 : index de saisonnalité
| Année | Trimestres | Total | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | 60 | 90 | 280 | 460 | 890 |
| 2 | 70 | 90 | 310 | 500 | 970 |
| 3 | 75 | 105 | 340 | 550 | 1070 |
| Total | 215 | 285 | 930 | 1510 | 2930 |
| Coef simple | 215/2930=0.07 | 285/2930=0.10 | 930/2930=0.32 | 1510/2930=0.51 | ∑ = 1 |
Étape 2 : Désaisonnaliser la prévision
Faire une prévision annuelle pour l'année suivante avec une des méthodes qui seront développées dans le chapitre suivant.
Ici, on va supposer qu'on a une prévision de 1200.
Étape 3 : Prévision saisonnalisée
Demande prévue au 1er trimestre = 0.07 * 1200 = 84
Demande prévue au 2ème trimestre = 0,10 * 1200 = 120
Demande prévue au 3ème trimestre = 0,32 * 1200 = 384
Demande prévue au 4ème trimestre = 0,51 * 1200 = 612
Demande totale prévue = 1200
Saisonnalité avec les coefficients saisonniers moyens
L'indice de saisonnalité indique le degré de variation de la moyenne de chaque trimestre sur le cycle annuel.
Exemple :
Étape 1 : index de saisonnalité
| Année | Trimestres | Moyenne | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | 60 | 90 | 280 | 460 | 222.5 |
| 2 | 70 | 90 | 310 | 500 | 242.5 |
| 3 | 75 | 105 | 340 | 550 | 267.5 |
| Moyenne | 71.6 | 95 | 310 | 503.3 | 244.2 |
| Coef simple | 71.6/244.2=0.29 | 95/244.2=0.38 | 310/244.2=1.27 | 503.3/244.2=2.06 | ∑ = 4 |
Étape 2 : Désaisonnaliser la prévision
Faire une prévision pour l'année suivante (on suppose ici 1200).
Désaisonnaliser la prévision = Distribuer la prévision annuelle uniformément sur les 4 trimestres.
Étape 3 : Prévision saisonnalisée
Demande prévue au 1er trimestre = 0.29 * 300 = 87
Demande prévue au 2ème trimestre = 0,38 * 300 = 114
Demande prévue au 3ème trimestre = 1.27 * 300 = 381
Demande prévue au 4ème trimestre = 2.06 * 300 = 618
Demande totale prévue = 1200
Prévision saisonnière avec tendance
Saisonnalité additive
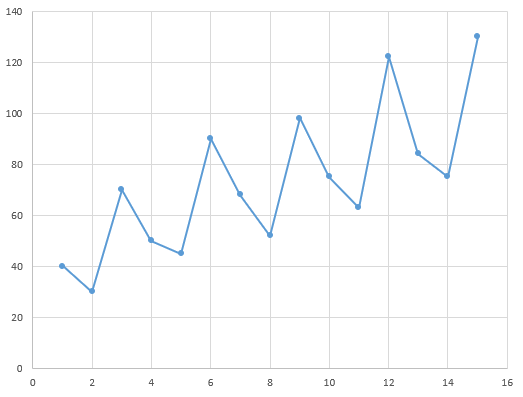
C'est le modèle adapté lorsque la saisonnalité s'additionne à la tendance.
yt = (a.t + b) + Ft
Saisonnalité multiplicative
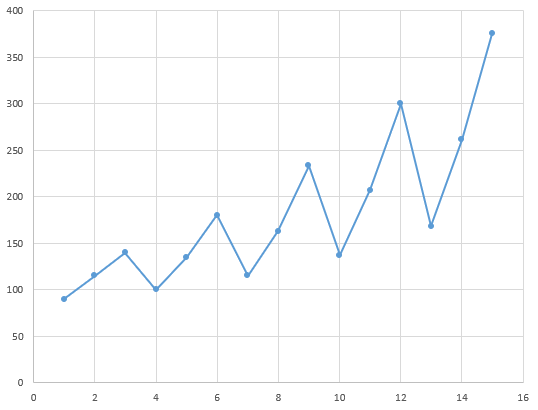
C'est le modèle adapté lorsque la saisonnalité est proportionnelle à la tendance.
yt = (a.t + b).Ft
Méthode de prévision avec saisonnalité et tendance
1. Lisser l'historique de données (le passé)
On utilise la moyenne mobile (MMt) pour effectuer le lissage.
L'ordre de la moyenne mobile est donné par les périodes de répétition de la saisonnalité (ex : 4 trimestres, 12 mois).
2. Calculer les coefficients saisonniers (S't)
- Méthode additive : S't = Dt - MMt
- Méthode multiplicative : S't = Dt / MMt
Avec S't : Coefficient saisonnier
Avec Dt : Demande réelle
3. Normaliser les coefficients (St)
On fait la moyenne des coefficients pour chaque saison : St
- Méthode additive : Soustraire la moyenne de ces moyennes à la moyenne saisionnière.
- Méthode multiplicative : Faire le produit en croix avec le nombre de saisons et la somme de ces moyennes.
4. Désaisonnaliser (CVSt)
- Méthode additive : CVSt = Dt - St
- Méthode multiplicative : CVSt = Dt / St
5. Calculer la tendance (Tt)
Le calcul de tendance se fait sur "CVSt" (y) par rapport à "t" (x).
6. Calculer la prévision (Pt) par application de la tendance et de la saisonnalité.
- Méthode additive : Pt = Tt + St
- Méthode multiplicative : Pt = Tt * St
7. Calculer l'erreur de prévision et
On analyse l'erreur pour tester la qualité de la prévision sur les périodes passées.
et = Pt - Dt