Méthodes de KING et KUZIAK
Méthodes de KUZIAK
Objectifs :
Recherche constante de la réactivité face aux besoins du marché pour une meilleure compétitivité.
- Simplifier ses flux pour faciliter le pilotage.
- Avoir une meilleure lisibilité des flux.
- Améliorer la gestion des flux en réduisant les trajets entre les postes, en éliminant les points d'engorgement, en évitant les retours en arrière, … pour augmenter la vitesse du flux.
- Minimiser les stocks d'en-cours, les manipulations.
- Améliorer les conditions de travail.
- Optimiser l'occupation des surfaces par une meilleure prise en compte des contraintes des bâtiments et des moyens de production (bruit, dimensions, sécurité, vibration, …) .
Méthodologie de détermination des ilots :
Déterminer des ilots est nécessaire lorsqu'on est confronté à des cas complexes.
- Grand nombre de produits, grand nombre de postes, nombreuses phases.
- Son domaine d'application est plus particulièrement les productions en ligne (production de masse : industrie automobile, etc.).
- Les implantations d'ateliers sont très souvent imposées par les gammes des différents produits.
- Par une étude systématique des gammes, on peut identifier des familles de pièces qui ont des flux similaires et regrouper les machines requises en ilots.
Définitions :
- Ilots de production
- Groupe de machines ayant la charge de la fabrication d'une famille de pièces et dont la disposition a été optimisée pour simplifier les flux de matière.
- Ilots indépendants
- Il n'existe pas de relation de flux entre les ilots.
- Ilots dépendants
- Il existe une relation de flux entre les ilots.
Exemple :
Pour illustrer cette démarche, prenons l'exemple d'un atelier de 18 postes de production (M1 à M18) permettant la réalisation de 8 produits (P1 à P8) parmi de nombreux autres produits.
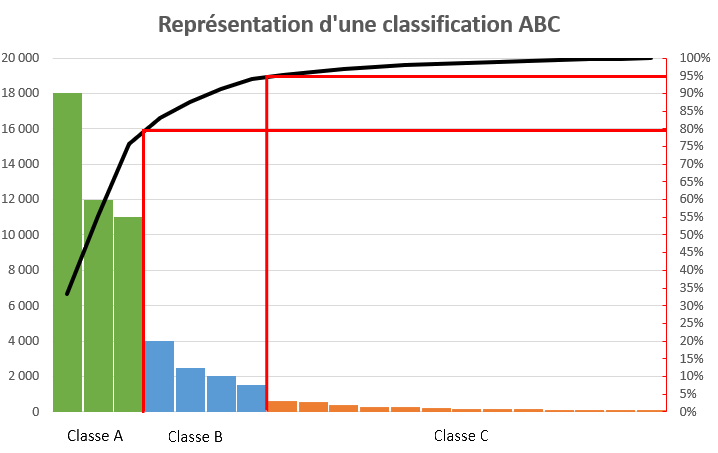
Les pièces P1 à P8 sont issues d'une classification ABC et représentent la classe A.
| Produits | Gamme / Phases | |||
|---|---|---|---|---|
| 10 | 20 | 30 | 40 | |
| P1 | M1 | M18 | M7 | M9 |
| P2 | M17 | M3 | M15 | M14 |
| P3 | M10 | M5 | M4 | M12 |
| P4 | M10 | M11 | M13 | M12 |
| P5 | M17 | M16 | M6 | M14 |
| P6 | M1 | M8 | M2 | |
| P7 | M16 | M5 | M6 | |
| P8 | M17 | M3 | M15 | M14 |
Sur cet exemple, proposer une solution théorique d'implantation d'atelier en respectant les objectifs et la méthodologie proposés ci-dessous.
Objectifs :
- Éviter les retours en arrière.
- Trois ilots maximum.
- Équilibrer le nombre de machines par ilot.
- Minimiser le parcours des pièces.
Méthodologie :
- Trouver les ilots indépendants avec l'algorithme de KUZIAK.
- Dans les ilots indépendants, chercher si nécessaire une partition de machine avec l'algorithme de KING.
- Implanter chaque ilot avec la méthode des antériorités.
- Représenter le schéma théorique d'implantation avec une implantation la plus optimisée possible en fonction des objectifs..
Tableau des affectations pièces machines.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 1 | 1 | 1 | 1 | ||||||||||||||
| P2 | 1 | 1 | 1 | 1 | ||||||||||||||
| P3 | 1 | 1 | 1 | 1 | ||||||||||||||
| P4 | 1 | 1 | 1 | 1 | ||||||||||||||
| P5 | 1 | 1 | 1 | 1 | ||||||||||||||
| P6 | 1 | 1 | 1 | |||||||||||||||
| P7 | 1 | 1 | 1 | |||||||||||||||
| P8 | 1 | 1 | 1 | 1 |
On met des « 1 » dans le tableau en fonction de la gamme des produits.
Algorithme de KUZIAK
- On sélectionne au hasard une pièce (exemple P1 : M1, M7, M9, M18).
- On barre la ligne P1.
- Puis on barre les colonnes qui correspondent aux « 1 » barrés.
- En barrant les colonnes, on va peut-être rencontrer d'autres liaisons machines – pièces avec d'autres « 1 » (dans ce cas P6).
- On recommence avec P6 le même processus qu'avec P1, etc ….
- Lorsqu'on ne rencontre plus de liaisons pièces – machines en barrant les colonnes, on recense les machines et les pièces validées..
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 1 | 1 | 1 | 1 | ||||||||||||||
| P2 | 1 | 1 | 1 | 1 | ||||||||||||||
| P3 | 1 | 1 | 1 | 1 | ||||||||||||||
| P4 | 1 | 1 | 1 | 1 | ||||||||||||||
| P5 | 1 | 1 | 1 | 1 | ||||||||||||||
| P6 | 1 | 1 | 1 | |||||||||||||||
| P7 | 1 | 1 | 1 | |||||||||||||||
| P8 | 1 | 1 | 1 | 1 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 1 | 1 | 1 | 1 | ||||||||||||||
| P2 | 1 | 1 | 1 | 1 | ||||||||||||||
| P3 | 1 | 1 | 1 | 1 | ||||||||||||||
| P4 | 1 | 1 | 1 | 1 | ||||||||||||||
| P5 | 1 | 1 | 1 | 1 | ||||||||||||||
| P6 | 1 | 1 | 1 | |||||||||||||||
| P7 | 1 | 1 | 1 | |||||||||||||||
| P8 | 1 | 1 | 1 | 1 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 1 | 1 | 1 | 1 | ||||||||||||||
| P2 | 1 | 1 | 1 | 1 | ||||||||||||||
| P3 | 1 | 1 | 1 | 1 | ||||||||||||||
| P4 | 1 | 1 | 1 | 1 | ||||||||||||||
| P5 | 1 | 1 | 1 | 1 | ||||||||||||||
| P6 | 1 | 1 | 1 | |||||||||||||||
| P7 | 1 | 1 | 1 | |||||||||||||||
| P8 | 1 | 1 | 1 | 1 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 1 | 1 | 1 | 1 | ||||||||||||||
| P2 | 1 | 1 | 1 | 1 | ||||||||||||||
| P3 | 1 | 1 | 1 | 1 | ||||||||||||||
| P4 | 1 | 1 | 1 | 1 | ||||||||||||||
| P5 | 1 | 1 | 1 | 1 | ||||||||||||||
| P6 | 1 | 1 | 1 | |||||||||||||||
| P7 | 1 | 1 | 1 | |||||||||||||||
| P8 | 1 | 1 | 1 | 1 |
Résultat : On détermine l'ilot 1.
Ilot 1 :
Machines : M1, M2, M7, M8, M9, M18
Pièces : P1, P6
Phase 2 : On sélectionne les lignes attachées aux colonnes sélectionnées.
Pour séparer des ilots éventuellement rattachés entre eux par une machine, on ne prend dans un ilot que les pièces qui ont au moins 50% des machines déjà rattachées à celui-ci.
On recommence avec P2 et on intègre P8 (4 machines sur 4), P5 (2 machines sur 4).
Puis P7 ( 2 machines sur 3) … mais pas P3 (1 machine sur 4).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 1 | 1 | 1 | 1 | ||||||||||||||
| P2 | 1 | 1 | 1 | 1 | ||||||||||||||
| P3 | 1 | 1 | 1 | 1 | ||||||||||||||
| P4 | 1 | 1 | 1 | 1 | ||||||||||||||
| P5 | 1 | 1 | 1 | 1 | ||||||||||||||
| P6 | 1 | 1 | 1 | |||||||||||||||
| P7 | 1 | 1 | 1 | |||||||||||||||
| P8 | 1 | 1 | 1 | 1 |
Puis les verticales...
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 1 | 1 | 1 | 1 | ||||||||||||||
| P2 | 1 | 1 | 1 | 1 | ||||||||||||||
| P3 | 1 | 1 | 1 | 1 | ||||||||||||||
| P4 | 1 | 1 | 1 | 1 | ||||||||||||||
| P5 | 1 | 1 | 1 | 1 | ||||||||||||||
| P6 | 1 | 1 | 1 | |||||||||||||||
| P7 | 1 | 1 | 1 | |||||||||||||||
| P8 | 1 | 1 | 1 | 1 |
On remarque qu'on croise les produits 5, 7 et 8.
Pour repartir avec les horizontales, la règle est qu'il ne faut considérer que les pièces dont les machines sont déjà barrées à au mois 50% en nombre.
Ce qui signifie que le produit transite déjà par ces machines, donc elles seront bien dans l'ilot qu'on est en train de constituer.
Dans notre cas, on va vérifier si c'est le cas pour les trois produits 5,7 et 8.
Produit 5 :
Deux machines non croisées (6 et 16), et deux machines déjà croisées (14 et 17). On a donc 2 sur 4, c'est-à-dire 50%.
Donc on pourra barrer ce produit.
Produit 7 :
Deux machines non croisées (5 et 6), et une machine déjà croisée (15). On a donc 1 sur 3, c'est-à-dire 33%, donc moins de 50% !
Donc on ne barrera pas ce produit.
Produit 8 :
Quatre machines déjà croisées (3, 14, 15 et 17). On a donc 4 sur 4, c'est-à-dire 100%.
Comme c'est 100% des machines qui sont déjà utilisées pour cet ilot, on n'aura plus à s'en occuper. Donc on peut barrer ce produit.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 1 | 1 | 1 | 1 | ||||||||||||||
| P2 | 1 | 1 | 1 | 1 | ||||||||||||||
| P3 | 1 | 1 | 1 | 1 | ||||||||||||||
| P4 | 1 | 1 | 1 | 1 | ||||||||||||||
| P5 | 1 | 1 | 1 | 1 | ||||||||||||||
| P6 | 1 | 1 | 1 | |||||||||||||||
| P7 | 1 | 1 | 1 | |||||||||||||||
| P8 | 1 | 1 | 1 | 1 |
On va maintenant s'occuper du produit P5. On barre donc sa ligne.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 1 | 1 | 1 | 1 | ||||||||||||||
| P2 | 1 | 1 | 1 | 1 | ||||||||||||||
| P3 | 1 | 1 | 1 | 1 | ||||||||||||||
| P4 | 1 | 1 | 1 | 1 | ||||||||||||||
| P5 | 1 | 1 | 1 | 1 | ||||||||||||||
| P6 | 1 | 1 | 1 | |||||||||||||||
| P7 | 1 | 1 | 1 | |||||||||||||||
| P8 | 1 | 1 | 1 | 1 |
On rencontre les machines 6 et 16. On barre alors les verticales correspondantes.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 1 | 1 | 1 | 1 | ||||||||||||||
| P2 | 1 | 1 | 1 | 1 | ||||||||||||||
| P3 | 1 | 1 | 1 | 1 | ||||||||||||||
| P4 | 1 | 1 | 1 | 1 | ||||||||||||||
| P5 | 1 | 1 | 1 | 1 | ||||||||||||||
| P6 | 1 | 1 | 1 | |||||||||||||||
| P7 | 1 | 1 | 1 | |||||||||||||||
| P8 | 1 | 1 | 1 | 1 |
On rencontre le produit P7. On continuera avec lui seulement si au moins 50% des machines sont déjà barrées.
Et c'est le cas, puisqu'on a deux machines (6 et 15) sur trois (la 5 n'étant pas barrée).
On a 66%, on doit donc continuer en barrant la ligne 7.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 1 | 1 | 1 | 1 | ||||||||||||||
| P2 | 1 | 1 | 1 | 1 | ||||||||||||||
| P3 | 1 | 1 | 1 | 1 | ||||||||||||||
| P4 | 1 | 1 | 1 | 1 | ||||||||||||||
| P5 | 1 | 1 | 1 | 1 | ||||||||||||||
| P6 | 1 | 1 | 1 | |||||||||||||||
| P7 | 1 | 1 | 1 | |||||||||||||||
| P8 | 1 | 1 | 1 | 1 |
On croise la machine 5, les autres sont déjà barrées. On trace donc la verticale pour cette machine.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 1 | 1 | 1 | 1 | ||||||||||||||
| P2 | 1 | 1 | 1 | 1 | ||||||||||||||
| P3 | 1 | 1 | 1 | 1 | ||||||||||||||
| P4 | 1 | 1 | 1 | 1 | ||||||||||||||
| P5 | 1 | 1 | 1 | 1 | ||||||||||||||
| P6 | 1 | 1 | 1 | |||||||||||||||
| P7 | 1 | 1 | 1 | |||||||||||||||
| P8 | 1 | 1 | 1 | 1 |
On croise le produit P3 uniquement.
Pour repartir, il faudrait au moins 50% des machines déjà barrées pour la ligne 3. Or c'est une seule sur quatre, c'est-à-dire 25%. Donc on s'arrête.
Comme on a traité tous les produits et toutes les machines y étant rattachées, on peut donc consituer le prochain ilot.
Résultat : On détermine l'ilot 2.
Ilot 2 :
Machines : M3, M5, M6, M14, M15, M16, M17
Pièces : P2, P5, P7, P8
Avantages de l'algorithme de KUZIAK.
L'algorithme de Kuziak est très rapide, notre exemple as a été traité en très peu de temps.
Il reste maintenant à terminer la procédure pour vérifier si un autre ilot ne devrait pas être créé en plus de celui qui reste.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 1 | 1 | 1 | 1 | ||||||||||||||
| P2 | 1 | 1 | 1 | 1 | ||||||||||||||
| P3 | 1 | 1 | 1 | 1 | ||||||||||||||
| P4 | 1 | 1 | 1 | 1 | ||||||||||||||
| P5 | 1 | 1 | 1 | 1 | ||||||||||||||
| P6 | 1 | 1 | 1 | |||||||||||||||
| P7 | 1 | 1 | 1 | |||||||||||||||
| P8 | 1 | 1 | 1 | 1 |
On commence par barrer la ligne 3.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 1 | 1 | 1 | 1 | ||||||||||||||
| P2 | 1 | 1 | 1 | 1 | ||||||||||||||
| P3 | 1 | 1 | 1 | 1 | ||||||||||||||
| P4 | 1 | 1 | 1 | 1 | ||||||||||||||
| P5 | 1 | 1 | 1 | 1 | ||||||||||||||
| P6 | 1 | 1 | 1 | |||||||||||||||
| P7 | 1 | 1 | 1 | |||||||||||||||
| P8 | 1 | 1 | 1 | 1 |
On croise les machines 4, 5, 10 et 12.
On trace les verticales.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 1 | 1 | 1 | 1 | ||||||||||||||
| P2 | 1 | 1 | 1 | 1 | ||||||||||||||
| P3 | 1 | 1 | 1 | 1 | ||||||||||||||
| P4 | 1 | 1 | 1 | 1 | ||||||||||||||
| P5 | 1 | 1 | 1 | 1 | ||||||||||||||
| P6 | 1 | 1 | 1 | |||||||||||||||
| P7 | 1 | 1 | 1 | |||||||||||||||
| P8 | 1 | 1 | 1 | 1 |
On croise les machines 10 et 12 pour le produit P4 mais pas les 11 et 13.
Ce qui fait deux sur quatre donc 50%, donc on continue.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 1 | 1 | 1 | 1 | ||||||||||||||
| P2 | 1 | 1 | 1 | 1 | ||||||||||||||
| P3 | 1 | 1 | 1 | 1 | ||||||||||||||
| P4 | 1 | 1 | 1 | 1 | ||||||||||||||
| P5 | 1 | 1 | 1 | 1 | ||||||||||||||
| P6 | 1 | 1 | 1 | |||||||||||||||
| P7 | 1 | 1 | 1 | |||||||||||||||
| P8 | 1 | 1 | 1 | 1 |
On a bien toutes les machines et tous les produits.
Résultat : On détermine l'ilot 3.
Ilot 3 :
Machines : M4, M5, M10, M11, M12, M13
Pièces : P3, P4
On remarquera que nous avons la machine M5 dans les ilots 2 et 3.
La machine M5 doit être dédoublée si on veut rendre les îlots indépendants.
Bien sûr, le critère de choix pour ce dédoublement reste la charge de cette machine !
Méthodes de KING
La méthode de King est plus rigoureuse que la méthode de Kuziak.
La machine M5 étant partagée entre deux ilots, on va repartir de là pour déterminer dans quel ilot il serait idéal de la placer.
Il n'y avait aucune ambiguité sur l'ilot 1, nous n'avons donc plus besoin de l'étudier.
Il reste donc les machines M3, M4, M5, M6, M10, M11, M12, M13, M14, M15, M16, M17.
Et les produits P2, P3, P4, P5, P7 et P8.
Méthodologie
- On va reconstruire une matrice comme pour la méthode de KUZIAK. On mettra les machines en ligne et les pièces en colonne.
- Ensuite, on va traduire la matrice en écriture binaire en affectant un poids en puissance de 2 à chacune des pièces.
- On ordonne les lignes dans l'ordre décroissant de l'équivalent décimal. En cas d'égalité, on respecte l'ordre des machines.
- On suit alors le même processus, mais sur les colonnes.
- Puis on recommence le même processus sur les lignes.
Première itération.
Les puissances de 2 sont classées du plus grand au plus petit (en dernier vous avez toujours 20 qui est égal à 1 !).
Dans la tableau on inscrit des "1" dans chaque case concernée par le produit.
Pour la pièce P2, la gamme nous indique qu'elle passe par les machines 17, 3, 15 et 14.
On va donc trouver des "1" à l'intersection de P2 et 3, puis P2 et 14, puis P2 et 15 et enfin P2 et 17.
Ensuite on additionne les nombres correspondant dans la table des puissances de 2.
Pour la pièce P2 ce sera : 2048 + 8 + 4 + 1 = 2061; Et ainsi de suite pour les autres pièces.
| 211 | 210 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2048 | 1024 | 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 3 | 4 | 5 | 6 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P2 | 1 | 1 | 1 | 1 | 2061 | ||||||||
| P3 | 1 | 1 | 1 | 1 | 1696 | ||||||||
| P4 | 1 | 1 | 1 | 1 | 240 | ||||||||
| P5 | 1 | 1 | 1 | 1 | 267 | ||||||||
| P7 | 1 | 1 | 1 | 770 | |||||||||
| P8 | 1 | 1 | 1 | 1 | 2061 |
Deuxième itération.
Avant de commencer la deuxième itération, vous devez d'abord réordonner les lignes en commençant par celle ayant obtenu le plus grand "coefficient" jusqu'au plus petit.
Donc, dans notre exemple, on va classer P2 (2061), puis P8 (2061), puis P3 (1696), P7 (770), P5 (267) et P4 (240).
On additionne maintenant suivant les colonnes.
Pour la machine 3, la pièce P2 vaut 32 et la pièce P8 vaut 16. On obtient donc 32 + 16 = 48.
| 2 | 3 | 4 | 5 | 6 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P2 | 1 | 1 | 1 | 1 | 32 | 25 | |||||||||
| P8 | 1 | 1 | 1 | 1 | 16 | 24 | |||||||||
| P3 | 1 | 1 | 1 | 1 | 8 | 23 | |||||||||
| P7 | 1 | 1 | 1 | 4 | 22 | ||||||||||
| P5 | 1 | 1 | 1 | 1 | 2 | 21 | |||||||||
| P4 | 1 | 1 | 1 | 1 | 1 | 20 | |||||||||
| 48 | 8 | 12 | 6 | 9 | 1 | 9 | 1 | 50 | 48 | 6 | 50 |
Troisième itération.
On classe cette fois-ci les machines (donc les colonnes) par ordre décroissant de "coefficent".
Ce qui, dans notre exemple, correspond aux machines : 14, puis 17, puis 3, 15, 5, 10, 12, 4, 6, 16, 11 et 13.
| 211 | 210 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2048 | 1024 | 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 3 | 14 | 17 | 3 | 15 | 5 | 10 | 12 | 4 | 6 | 16 | 11 | 13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P2 | 1 | 1 | 1 | 1 | 3840 | ||||||||
| P8 | 1 | 1 | 1 | 1 | 3840 | ||||||||
| P3 | 1 | 1 | 1 | 1 | 240 | ||||||||
| P7 | 1 | 1 | 1 | 142 | |||||||||
| P5 | 1 | 1 | 1 | 1 | 3084 | ||||||||
| P4 | 1 | 1 | 1 | 1 | 99 |
Et ainsi de suite jusqu'à la sixième itération.
Sixième itération.
| 6 | 14 | 17 | 3 | 15 | 6 | 16 | 5 | 10 | 12 | 4 | 11 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P2 | 1 | 1 | 1 | 1 | ||||||||
| P8 | 1 | 1 | 1 | 1 | ||||||||
| P5 | 1 | 1 | 1 | 1 | ||||||||
| P7 | 1 | 1 | 1 | |||||||||
| P3 | 1 | 1 | 1 | 1 | ||||||||
| P4 | 1 | 1 | 1 | 1 |
On peut donc proposer de mettre le machine 5 dans l'ilot 3 et la pièce 7 va donc passer d'un ilot à l'autre.
| 6 | 14 | 17 | 3 | 15 | 6 | 16 | 5 | 10 | 12 | 4 | 11 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P2 | 1 | 1 | 1 | 1 | ||||||||
| P8 | 1 | 1 | 1 | 1 | ||||||||
| P5 | 1 | 1 | 1 | 1 | ||||||||
| P7 | 1 | 1 | 1 | |||||||||
| P3 | 1 | 1 | 1 | 1 | ||||||||
| P4 | 1 | 1 | 1 | 1 |
Résultat :
Ilot 1 :
Machines : M1, M2, M7, M8, M9, M18
Pièces : P1, P6
Ilot 2 :
Machines : M3, M6, M14, M15, M16, M17
Pièces : P2, P5, P8 et P7
Ilot 3 :
Machines : M4, M5, M10, M11, M12, M13
Pièces : P3, P4 et P7